what is it?
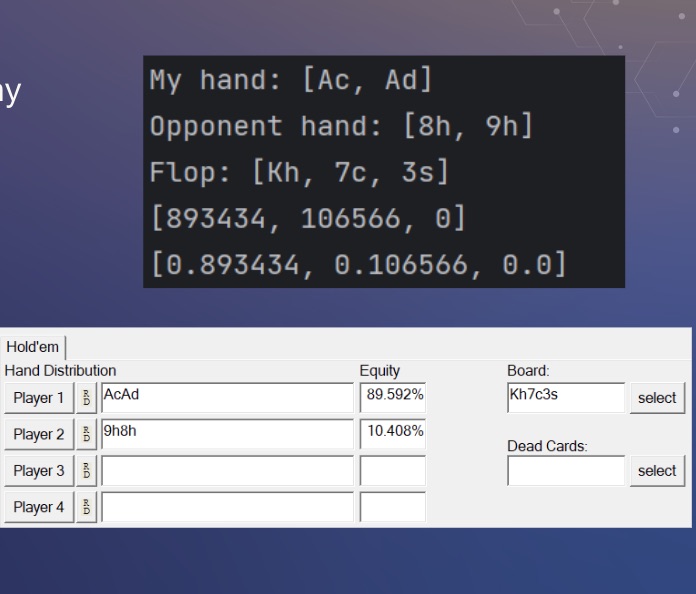
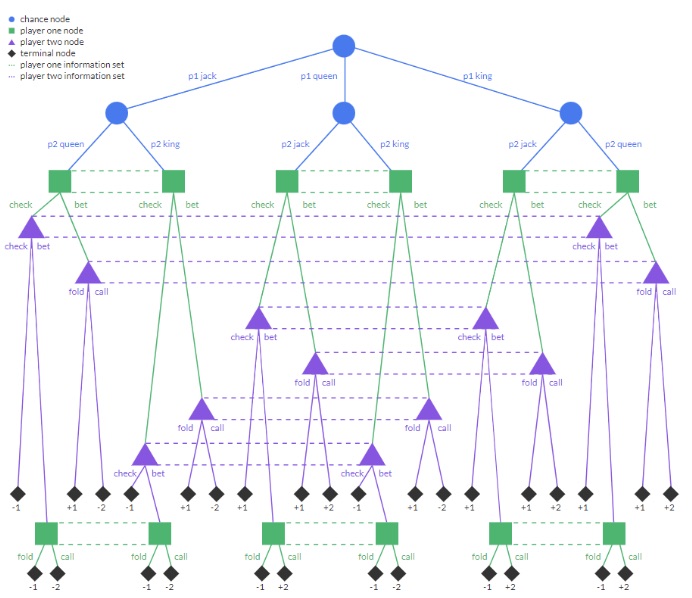
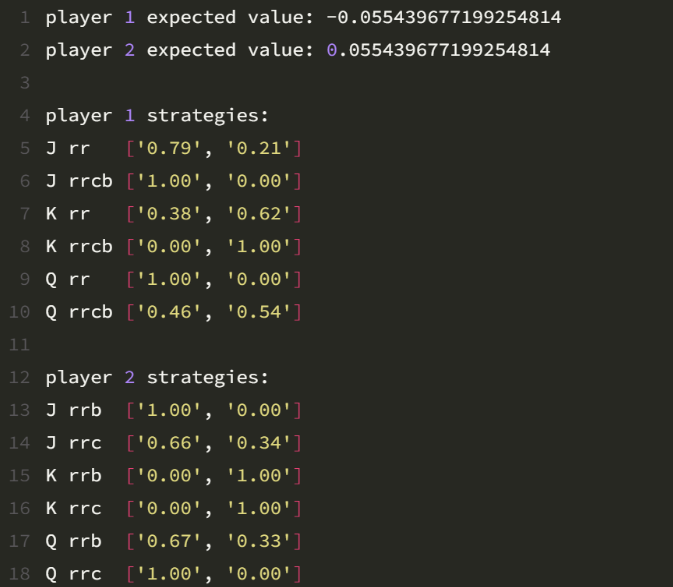
We first created a monte carlo simulator that would work for poker games for up to 10 players, calculating equity with different hands as inputs. Some of the features we had to implement efficiently included being able to deal from a deck of cards, the ability to shuffle, and hand evaluation. Once we had this aspect working, we began delving into game theory concepts such as regret matching (using accumulated regrets from past hands to adjust its decision-making process) and counterfactual regret minimization (a further advancement). We ran this on Kuhn Poker to evaluate the results.
cool things/ what i learned
along the way, I studied a good deal of poker theory to help facilitate the building:
- pot odds, implied odds
- kuhn's poker
- nash equilibrium
shuffling function: instead of using the brute force method, we used fisher-yates:
- swaps the last element and a randomly selected element from the whole array
- iterates from array index n-1 to 1
- creates am even distribution of a card at a particular spot in the deck so all permutations are equally likely
- reduces time complexity to O(n) from O(n^2)
hand evaluation: how do we represent the value of a hand?? hash code-- to get a unique number for each combination of cards. but how much do we actually have to know about the hand? we don't want to sort the hand, that requires computation during decision-making solution: rank evaluation
- we used bitmasks to create a perfect hash
- we pre-computerd a unique hash for every single card and rank using bits masks, creating lookup tables for easy access during decision-making
- creates am even distribution of a card at a particular spot in the deck so all permutations are equally likely